Paper Title: Mapping Hebbian Learning Rules to Coupling Resistances for Oscillatory Neural Networks

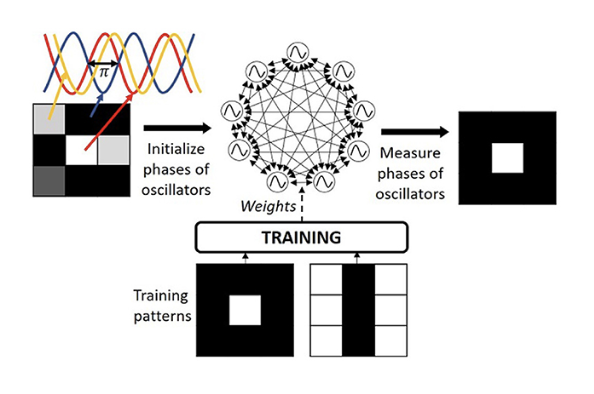
Oscillatory Neural Network (ONN) is an emerging neuromorphic architecture with oscillators representing neurons and information encoded in oscillator’s phase relations. In an ONN, oscillators are coupled with electrical elements to define the network’s weights and achieve massive parallel computation. As the weights preserve the network functionality, mapping weights to coupling elements plays a crucial role in ONN performance. In this work, we investigate relaxation oscillators based on VO₂ material, and we propose a methodology to map Hebbian coefficients to ONN coupling resistances, allowing a large-scale ONN design. We develop an analytical framework to map weight coefficients into coupling resistor values to analyze ONN architecture performance. We report on an ONN with 60 fully-connected oscillators that perform pattern recognition as a Hopfield Neural Network.